Обзор материнской платы gigabyte ga-z87mx-d3h

Замкнется ли эта вычислительная машина по «кругу»? Первое доказательство Тьюринга

На проблему Entscheidungsproblem , проблему принятия решения , Черч впервые дал ответ в апреле 1935 года и опередил Тьюринга более чем на год, так как статья Тьюринга была получена для публикации в мае 1936 года (также поступившая для публикации в 1936 году — в октябре, позже, чем работа Тьюринга — была получена. короткая статья Эмиля Поста, в которой обсуждалась редукция алгоритма к простому машинному «методу», очень похожему на модель вычислительной машины Тьюринга (подробности см. в машине Пост-Тьюринга ).
Доказательство Тьюринга затруднено из-за количества требуемых определений и его тонкости. См машина Тьюринга и доказательство Тьюринга для деталей.
Первое доказательство Тьюринга (из трех) следует схеме парадокса Ричарда: вычислительная машина Тьюринга — это алгоритм, представленный строкой из семи букв в «вычислительной машине». Его «вычисление» состоит в том, чтобы проверить все вычислительные машины (включая себя) на наличие «кругов» и сформировать диагональное число из вычислений некруговых или «успешных» вычислительных машин. Он делает это, начиная с 1, путем преобразования чисел (основание в строки из семи букв для проверки. Когда он достигает своего собственного номера, он создает свою собственную буквенную строку. Он решает, что это буквенная строка успешной машины, но когда он пытается выполнить вычисления этой машины ( свои собственные ), он замыкается по кругу и не может продолжить. Таким образом, мы пришли к парадоксу Ричарда. (Если вы сбиты с толку, см. Доказательство Тьюринга).

Ряд аналогичных доказательств неразрешимости появился вскоре до и после доказательства Тьюринга:

Апрель 1935 года: Доказательство Алонзо Черча («Неразрешимая проблема элементарной теории чисел»). Его доказательство заключалось в том, чтобы «… предложить определение эффективной вычислимости … и показать на примере, что не каждая проблема этого класса разрешима» (Undecidable, стр. 90))
1946: проблема почтовой корреспонденции (см. Хопкрофт и Ульман, стр. 193 и далее, стр. 407 для справки)
Апрель 1947: Доказательство Эмиля Поста ( Рекурсивная неразрешимость проблемы Туэ ) (Неразрешимая стр. 293). С тех пор это стало известно как «проблема слова Туэ» или «проблема слова Туэ» ( Аксель Туэ предложил эту проблему в статье 1914 года (см. Ссылки на статью Поста в Undecidable, стр. 303)).
Теорема Райса : обобщенная формулировка второй теоремы Тьюринга (см. Хопкрофт и Ульман, стр. 185 и далее)
Теорема Грейбаха : неразрешимость в теории языков (см. Хопкрофт и Ульман, стр. 205ff и ссылку на стр. 401, там же: Грейбах «Неразрешимость проблемы неоднозначности для минимальных линейных грамматик», Информация и контроль 6: 2, 117–125 , также ссылка на стр. 402 там же: Greibach «Заметка о неразрешимых свойствах формальных языков», Math Systems Theory 2: 1, 1–6.)
Вопросы о плитках Пенроуза
Вопрос о решениях диофантовых уравнений и результирующий ответ в теореме MRDP; см. запись ниже.

Можно ли доказать эту теорему на основе этих аксиом? Доказательство Гёделя

По словам Нагеля и Ньюмана (стр. 68), «статья Гёделя трудна. Прежде чем будут достигнуты основные результаты, необходимо усвоить 46 предварительных определений вместе с несколькими важными предварительными теоремами» (стр. 68). Фактически, Нагелю и Ньюману потребовалось 67-страничное введение для изложения доказательства. Но если читатель чувствует себя достаточно сильным, чтобы взяться за работу, Мартин Дэвис замечает, что «эта замечательная статья является не только интеллектуальной вехой, но и написана с ясностью и энергией, которые делают чтение приятным» (Дэвис в Undecidable, p. 4). Большинству читателей рекомендуется сначала увидеть Нагеля и Ньюмана.

Так что же доказал Гёдель? По его собственным словам:

«Разумно … сделать гипотезу, что … [] аксиомы … достаточны для решения всех математических вопросов, которые могут быть формально выражены в данных системах. будет показано, что это не так, а, скорее, что … существуют относительно простые проблемы теории обычных целых чисел, которые не могут быть решены на основе аксиом »(Гедель в Undecidable, стр. 4).

Гёдель сравнил свое доказательство с «антиномией Ричарда» (« антиномия » — это противоречие или парадокс; подробнее см . Парадокс Ричарда ):

«Сразу очевидна аналогия этого результата с антиномией Ричарда; существует также тесная связь с парадоксом лжецов (сноска 14 Гёделя: каждая эпистемологическая антиномия может использоваться для аналогичного доказательства неразрешимости) … Таким образом, мы имеем представленное нам предложение, которое утверждает свою собственную недоказуемость . (Его сноска 15: Вопреки внешнему виду, такое предложение не является круговым, поскольку для начала оно утверждает недоказуемость вполне определенной формулы) »(Гёдель в Undecidable , стр.9).

Нейромодуль для материнской платы ПК

Как выяснил CNews, отечественный научно-технический центр (НТЦ) «Модуль», известный разработками нейропроцессоров, создал нейросетевой вычислитель, который можно подключить в стандартный слот расширения PCIe на материнской плате компьютера.

Новинка получила название NM Card. Разработчики отмечают, что она позволит развернуть на компьютере нейросеть для решения задач цифровой обработки сигналов и изображений.

Областями применения помимо цифровой обработки сигналов и изображений заявлены искусственный интеллект, специализированные высокопроизводительные вычислительные комплексы, облачная обработка данных, системы машинного зрения, робототехника, телекоммуникационные и связные системы, образование.

Нейромодулm NM Card

На момент выхода публикации «Модуль» не смог объяснить CNews, доступен ли на данный момент вычислитель только на уровне опытных образцов или уже выпускается серийно. Также остались без ответа вопросы о планируемых тиражах, о том, кого в компании считают перспективными клиентами, есть ли уже у новинки конкретные заказчики и о том, какого конкретно эффекта с помощью новинки могут достичь пользователи.

Упаковка, комплект поставки

GIGABYTE GA-Z87MX-D3H балансирует на грани между бюджетным и началом среднего ценового сегмента. Ориентировочная стоимость на момент подготовки материала составляет порядка $150 (1250 грн.)

О некоторых претензиях платы говорят синие вставки радиаторов, выделенные в дизайнерском оформлении упаковки. Как вы помните, привязка к цвету в линейке современных решений GIGABYTE несет вполне конкретную смысловую нагрузку. Эта модель поставляется в компактной коробке, выполненной в характерных для производителя черных тонах.

В комплект поставки входят:

— руководство по эксплуатации и диск с драйверами;

— заглушка на заднюю панель корпуса;

— четыре SATA-кабеля;

— SLI-мостик.

Вполне неплохо как для недорогого продукта.

Невозможные конструкции, которые искали древние греки

Три известных вопроса греческой геометрии заключались в следующем:

… с циркулем и линейкой, чтобы разрезать пополам под любым углом ,
построить куб с объемом, вдвое превышающим объем данного куба
построить квадрат, равный по площади квадрату данного круга.

Более 2000 лет предпринимались безуспешные попытки решить эти проблемы; наконец, в XIX веке было доказано, что искомые конструкции логически невозможны.

Четвертая проблема древних греков заключалась в том, чтобы построить равносторонний многоугольник с заданным числом сторон n , помимо базовых случаев n = 3, 4, 5, которые они знали, как построить.

Все это проблемы евклидовой конструкции , а евклидовы конструкции могут быть выполнены, только если они включают только евклидовы числа (по определению последнего) (Харди и Райт, стр. 159). Иррациональные числа могут быть евклидовыми. Хорошим примером является иррациональное число квадратный корень из 2. Это просто длина гипотенузы прямоугольного треугольника с катетами равной единице длины, и его можно построить с помощью линейки и циркуля. Но спустя столетия после Евклида было доказано, что евклидовы числа не могут включать никаких операций, кроме сложения, вычитания, умножения, деления и извлечения квадратных корней.

Трисекция угла и удвоение куба

Как деление на три части общего угла, так и удвоение куба требуют извлечения кубических корней , которые не могут быть построены с помощью циркуля и линейки.

Квадрат круга

Существует доказательство, демонстрирующее, что любое евклидово число является алгебраическим числом — числом, которое является решением некоторого полиномиального уравнения . Следовательно, поскольку в 1882 году было доказано, что оно является трансцендентным числом и, следовательно, по определению не является алгебраическим числом, оно не является евклидовым числом. Следовательно, построить длину из единичной окружности невозможно, и окружность нельзя возвести в квадрат.
π{\ displaystyle \ pi}π{\ displaystyle \ pi}

Плата в работе

Возможности ранее изученной на примере других материнских плат GIGABYTE программной оболочки EasyTune достаточно обширны. Эта утилита позволяет настраивать систему, управлять параметрами энергосбережения и скорости вращения вентиляторов.

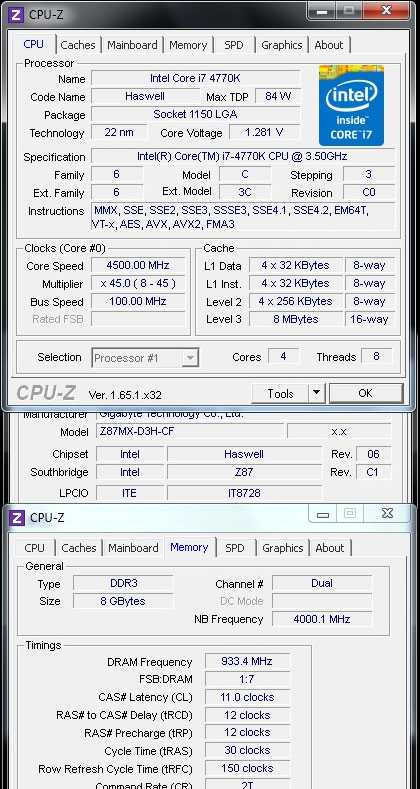
Рассматриваемая модель оказалась достаточно стабильной и предсказуемой при изменении базовых настроек. Форсировать наш тестовый процессор до максимально возможных при воздушном охлаждении 4,6 ГГц ей еще под силу.

При активации автоматических профилей разгона, доступных как в UEFI, так и через EasyTune, нам покорились только 4,5 ГГц:

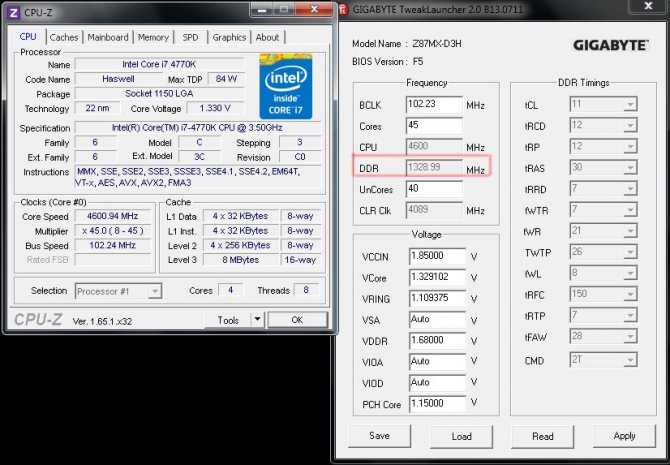
GA-Z87MX-D3H отлично чувствует себя при настройке подсистемы оперативной памяти – тестовый комплект DRAM стабильно функционировал на частотах порядка 2660 МГц:

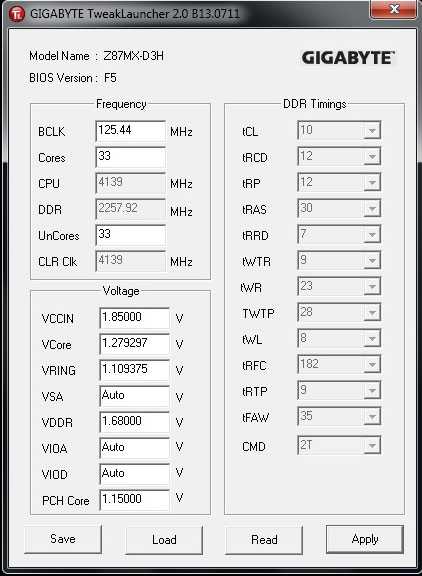
Разгон по BCLK также возможен, однако с последней на момент подготовки этого материала версией UEFI – F5 – наш экземпляр платы был способен на загрузку ОС лишь с делителем 1,25:

Повышение базовой частоты при делителе 1.0 возможно в пределах порядка 3–3,5 МГц.

В случае использования материнской платы GIGABYTE GA-Z87MX-D3H следует иметь ввиду несколько ограничений, накладываемых компоновкой РСВ. Так, у владельцев габаритных кулеров могут возникнуть сложности с их установкой. К примеру, Thermalright Archon при классической ориентации «на выдув» упирался ребрами в обратную сторону графического адаптера, хотя с Scythe MUGEN 3 подобных нюансов не возникло.

Слоты ОЗУ слегка блокируются габаритной видеокартой, хотя при желании достать память еще можно.

Нагрев штатных радиаторов – в пределах нормы. Температура силового в процессе испытаний находилась на уровне примерно 50 °С, чипсетного – 55 °С.

В целом рассматриваемая плата оставила после себя неплохие впечатления. В любом случае потраченные на покупку деньги она с лихвой компенсирует.

Возможность сэкономить сохраняется

Как пишет VideoCardz, Intel намерена выпускать свои настольные Alder Lake-S в коробочном (боксовом) исполнении. Такая комплектация включает, помимо самого процессора, еще и стандартный маломощный кулер, производительности которого хватает только на отвод тепла от процессора, работающего на штатных частотах.

Комплектный кулер Intel, утверждает VideoCardz, с релизом Alder Lake-S не станет лучше или производительнее. Его радиатор по-прежнему будет алюминиевым, и пока неизвестно, имеется ли на его контактной площадке вставка из меди для лучшего отвода тепла.

Сторонние производители кулеров тоже могут облегчить пользователям процесс апгрейда и предложить им не полностью новую систему охлаждения, а специальные фирменные крепления, для нового сокета. Это распространенная практика.

Noctua NH-U9S

В примеру, в ассортименте компании Noctua есть кулер NH-U9S, в модификациях, выпускавшихся до 2019 г., непригодный для установки на процессоры AMD под сокет АМ4. Однако для них существуют фирменные переходные крепления NM-AM4-UxS, этот недочет устраняющий.

Крепления NM-AM4-UxS для сокета АМ4

Такой подход избавляет пользователя от необходимости покупки нового кулера. Тот же NH-U9S на момент публикации материала в российской рознице стоил 7000 руб. (по данным DNS), а дополнительные крепления – 540 руб.

Общая информация

1.Легко разгоняется
Gigabyte GA-Z87MX-D3H

Разгон системы — обычная, хоть и сложная процедура, но некоторые производители предусматривают кнопку или программу, в которых с одного нажатия можно разогнать компьютер и получить более высокую производительность.

2.Легко сбрасывать BIOS
Gigabyte GA-Z87MX-D3H

На задней панели материнской платы есть кнопка или тумблер для очистки памяти CMOS, который сбрасывает настройки BIOS на заводские. Эта функция применима в ситуациях, когда в BIOS что-то не так настроено, из-за чего компьютер не грузится. При этом не надо открывать корпус и искать джампер CMOS.

3.имеет Wi-Fi
Gigabyte GA-Z87MX-D3H

Устройство может подключаться к Wi-Fi.

4.Поддержка форсированной зарядки через USB
Gigabyte GA-Z87MX-D3H

Эта функция позволяет заряжать устройства (смартфоны, планшетники) быстрее чем через обычный USB-порт. Некоторые реализации позволяют заряжать устройства, даже если компьютер находится в режиме сна или выключен.

5.мульти-ГПУ

Количество графических процессоров, поддерживаемых при использовании мульти-GPU конфигурации. Использование нескольких GPU параллельно может дать более высокую производительность.

6.Есть Bluetooth
Gigabyte GA-Z87MX-D3H

Bluetooth — беспроводная технология, позволяющая с лёгкостью передавать данные между устройствами: смартфонами, планшетниками и компьютерами.

7.Поддержка турбо-режима USB.
Gigabyte GA-Z87MX-D3H

Этот режим предлагает более высокую скорость передачи данных через USB, сравнимую со скоростью внешнего жёсткого диска.

8.Интерфейс 802.11ac WiFi
Gigabyte GA-Z87MX-D3H

Беспроводной 802.11ac работает на частоте 5 ГГц, а также на 2,4 ГГц (двухдиапазонный WiFi). Предлагает более высокую скорость передачи данных, повышенную надёжность и более оптимальный принцип энергопотребления. Даёт преимущества для игр и видеопотоков HD.

9.поддерживает Wi-Fi 6 (802.11ax)
Gigabyte GA-Z87MX-D3H

Wi-Fi 6, выпущенный в 2019 году, основан на стандарте беспроводной сети IEEE 802.11ax. Разработанный для работы во всех полосах частот от 1 до 6 ГГц, он предлагает более высокие скорости передачи данных и меньшую задержку по сравнению с предыдущими технологиями Wi-Fi.

Особенности UEFI

UEFI-оболочка материнских плат GIGABYTE на базе Z87 Express кардинально отличается от того, к чему привыкли поклонники продукции этой компании. Мы уже останавливались на изучении прошивки в обзоре G1.Sniper 5, однако графический интерфейс сравнительно недорогих плат слегка отличается в сторону упрощения (хотя конфигурация разделов – та же).

«Домашняя» вкладка сходу приветствует пользователя базовыми настройками частот работы процессора и памяти, а также возможностью регулировки ключевых напряжений. В подменю Standard хранятся параметры работы встроенной графики и контроллера жестких дисков.

Пользователю доступна опция персонализации подменю под себя, однако даже базовые «разбор полетов» и настройка потребуют времени.

Вкладка Performance уже более понятна.

В ней доступны регулировки параметров частот (Frequency), установок ОЗУ (Memory), питающих напряжений (Voltage), состояния системы и температурных показателей (PC Health Status, Miscellaneous, CPU Status, Memory Status).

Системная вкладка позволяет установить пароль на UEFI, воспользоваться информативным календарем и задать системные дату-время.

BIOS Features – предельно прост и понятен.

Вкладка Peripherals содержит несколько подменю, привязанных к установкам дочерних контроллеров.

Power Management позволяет задать элементы энергосбережения и «научить» компьютер самостоятельно включаться в заданное время.

Если подобная конфигурация разделов вас пугает, непривычно тяжела – просто переключитесь на традиционное визуальное оформление оболочки.

Подобная раскладка хоть имеет схожее дерево подменю и ключевых настроек, гораздо проще и привычнее в восприятии и установке необходимых параметров, особенно если вы привыкли работать в UEFI с клавиатуры.

Пределы регулировки необходимых параметров устроят даже искушенных пользователей. Единственное, экстремальным оверклокерам может не хватить 1,8 В для максимального разгона CPU при его охлаждении жидким азотом, а вот DRAM – вполне (2,1 В). Для установки BCLK доступны варианты Strap 1.25 и 1.66.

Как это должно работать

По всей видимости, на технологическом уровне модуль стыкуется с ПК с помощью созданного компанией (для других модулей) комплекта аппаратных и программных средств для разработки и реализации глубоких нейронных сетей — NeuroMatrix DeepLearning (NMDL). Подтвердить или опровергнуть это предположение «Модуль» CNews не смог.

Именно NMDL был задействован в предыдущей новинке компании — нейровычислителе NM Stick, реализованном в форм-факторе флешки.

Значения производительности NM Card при вычислении некоторых современных глубоких нейронных сетей

На сайте «Модуля» указано, что NMDL состоит из двух частей. Одна часть работает на внешней системе под управлением 64-разрядных ОС Microsoft Windows 7/10 или Linux. Другая часть запускается и работает непосредственно на процессоре вычислительного модуля.

Композитный ИИ: что это такое и зачем он нужен?
Искусственный интеллект

NMDL выполняет обработку информации в соответствии с заданной моделью нейросети, он позволяет запускать предварительно обученную глубокую нейронную сеть на вычислительных модулях, говорится в описании разработчиков.

Из описаний сходных по некоторым параметрам других модулей НТЦ (в иных форм-факторах) можно заключить, что в случае с NM Stick мы имеем дело с так называемым одноплатным компьютером. В изделиях этого класса процессор интегрирован с различными контроллерами и обладает набором интерфейсов ввода-вывода. В общем случае они служат базисом для создания каких-либо полноценных компьютерных систем.

Виды доказательств невозможности

Доказательство от противного

Один из широко используемых типов доказательства невозможности — это доказательство от противного . В этом типе доказательства показано, что если бы что-то, например решение определенного класса уравнений, было возможно, то были бы истинными две взаимно противоречащие вещи, например, число, являющееся как четным, так и нечетным. Из противоречия следует, что исходная посылка невозможна.

Доказательство по происхождению

Один из типов доказательства от противоречия — это доказательство спуска, которое сначала начинается с предположения, что что-то возможно, например, положительное целочисленное решение некоторого класса уравнений, и, следовательно, должно быть наименьшее решение. Затем на основе предполагаемого наименьшего решения показано, что может быть найдено меньшее решение, что противоречит посылке о том, что первое решение было наименьшим из возможных, тем самым показывая, что исходная посылка (о существовании решения) должна быть ложной.

Существование иррациональных чисел: доказательство пифагорейцев

Доказательство Пифагора (или, что более вероятно, одного из его учеников) около 500 г. до н.э. оказало глубокое влияние на математику. Это показывает, что квадратный корень из 2 не может быть выражен как отношение двух целых чисел (подсчет чисел). В доказательстве «числа» разделились на два неперекрывающихся набора — рациональные числа и иррациональные числа . Это раздвоение было использовано Кантором в его диагональном методе , который , в свою очередь , был использован Тьюрингом в его доказательстве , что проблема разрешение , то проблема решения о Гильберте , неразрешима.

Доказательства последовали для различных квадратных корней из простых чисел до 17.

Теперь существует более общее доказательство того, что:

М х корней целого числа N является нерациональным, если N не являются м й степени целого числа п ».

То есть невозможно выразить корень m- й степени целого числа N как отношение a ⁄ b двух целых чисел a и b , которые не имеют общего простого множителя, за исключением случаев, когда b = 1.

Имеет ли это диофантово уравнение целочисленное решение? Десятая проблема Гильберта

На вопрос «Имеет ли произвольное« диофантово уравнение »целочисленное решение?» является неразрешимой .То есть, невозможно ответить на вопрос , для всех случаев.

Францен вводит десятую проблему Гильберта и теорему MRDP ( теорема Матиясевича-Робинсона-Дэвиса-Патнэма), которая утверждает, что «не существует алгоритма, который мог бы решить, имеет ли диофантово уравнение какое-либо решение». MRDP использует доказательство неразрешимости Тьюринга: «… набор разрешимых диофантовых уравнений является примером вычислимо перечислимого, но не разрешимого множества, а набор неразрешимых диофантовых уравнений не является вычислимо перечислимым» (стр. 71).

Замкнется ли эта вычислительная машина по «кругу»? Первое доказательство Тьюринга

На проблему Entscheidungsproblem , проблему принятия решения , Черч впервые дал ответ в апреле 1935 года и опередил Тьюринга более чем на год, так как статья Тьюринга была получена для публикации в мае 1936 года (также поступившая для публикации в 1936 году — в октябре, позже, чем работа Тьюринга — была получена. короткая статья Эмиля Поста, в которой обсуждалась редукция алгоритма к простому машинному «методу», очень похожему на модель вычислительной машины Тьюринга (подробности см. в машине Пост-Тьюринга ).
Доказательство Тьюринга затруднено из-за количества требуемых определений и его тонкости. См машина Тьюринга и доказательство Тьюринга для деталей.
Первое доказательство Тьюринга (из трех) следует схеме парадокса Ричарда: вычислительная машина Тьюринга — это алгоритм, представленный строкой из семи букв в «вычислительной машине». Его «вычисление» состоит в том, чтобы проверить все вычислительные машины (включая себя) на наличие «кругов» и сформировать диагональное число из вычислений некруговых или «успешных» вычислительных машин. Он делает это, начиная с 1, путем преобразования чисел (основание в строки из семи букв для проверки. Когда он достигает своего собственного номера, он создает свою собственную буквенную строку. Он решает, что это буквенная строка успешной машины, но когда он пытается выполнить вычисления этой машины ( свои собственные ), он замыкается по кругу и не может продолжить. Таким образом, мы пришли к парадоксу Ричарда. (Если вы сбиты с толку, см. Доказательство Тьюринга).

Ряд аналогичных доказательств неразрешимости появился вскоре до и после доказательства Тьюринга:

Апрель 1935 года: Доказательство Алонзо Черча («Неразрешимая проблема элементарной теории чисел»). Его доказательство заключалось в том, чтобы «… предложить определение эффективной вычислимости … и показать на примере, что не каждая проблема этого класса разрешима» (Undecidable, стр. 90))
1946: проблема почтовой корреспонденции (см. Хопкрофт и Ульман, стр. 193 и далее, стр. 407 для справки)
Апрель 1947: Доказательство Эмиля Поста ( Рекурсивная неразрешимость проблемы Туэ ) (Неразрешимая стр. 293). С тех пор это стало известно как «проблема слова Туэ» или «проблема слова Туэ» ( Аксель Туэ предложил эту проблему в статье 1914 года (см. Ссылки на статью Поста в Undecidable, стр. 303)).
Теорема Райса : обобщенная формулировка второй теоремы Тьюринга (см. Хопкрофт и Ульман, стр. 185 и далее)
Теорема Грейбаха : неразрешимость в теории языков (см. Хопкрофт и Ульман, стр. 205ff и ссылку на стр. 401, там же: Грейбах «Неразрешимость проблемы неоднозначности для минимальных линейных грамматик», Информация и контроль 6: 2, 117–125 , также ссылка на стр. 402 там же: Greibach «Заметка о неразрешимых свойствах формальных языков», Math Systems Theory 2: 1, 1–6.)
Вопросы о плитках Пенроуза
Вопрос о решениях диофантовых уравнений и результирующий ответ в теореме MRDP; см. запись ниже.

Дизайн и особенности компоновки

В отличие от ранее упомянутой GIGABYTE GA-B85-HD3, GA-H87-D3H подобно более дорогим платам построена с использованием компонентной базы Ultra Durable 5 Plus. Радиаторы имеют синие вставки, что согласно последней версии классификации производителя говорит о прицеле на сравнительно прогрессивного пользователя.

В то же время рассматриваемая модель имеет коричневую РСВ и до энтузиастского сегмента, с его всецело черными платами, не дотягивает.

GA-H87-D3H выполнена в форм-факторе АТХ (305×225 мм). При первом взгляде на плату создается впечатление, что перед нами – младшее решение на базе Intel Z87. Помимо оформления радиаторов к этому подталкивает наличие двух полноразмерных PCI-Express и общий стиль исполнения. К слову, взгляните еще раз на фото комплекта поставки (а именно на обложку руководства по эксплуатации).

Четырехфазная силовая подсистема аналогична используемой в GA-Z87MX-D3H и выполнена на базе контроллера IR3564B и мосфет-сборок IR3553M. Если помните, в GA-B85-HD3 на этом участке платы применяется компонентная база предыдущего поколения.

На заднюю панель рассматриваемой модели вынесены:

— PS/2;

— четыре USB 3.0;

— четыре USB 2.0;

— RJ45;

— HDMI, DVI-D, D-Sub;

— пять разъемов аудиоджек;

— оптический S/PDIF

Весьма неплохо как для бюджетного решения. Звуковая подсистема реализована на базе проверенного временем HDA-кодека Realtek ALC892, часто используемого в недорогих продуктах.

За работу гигабитной сети отвечает чипсет в связке с кодеком Intel.

В современных материнских платах GIGABYTE реализована технология DualBIOS, подразумевающая наличие двух микросхем для хранения кода прошивки.

Примечательно, что коннекторы передней панели имеют цветовую маркировку. Сброс настроек CMOS осуществляется привычным для продуктов GIGABYTE способом – для этого необходимо замкнуть два контакта, находящиеся внизу РСВ.

На плате применяются порты SATA, распаянные перпендикулярно к печатной плате. Учитывая их максимальное смещение в нижний угол, подобное решение не всегда будет достаточно удобным. SATA-интерфейс реализован силами чипсета, поэтому имеет стандартную пропускную способность – 6 Гб/с для каждого порта.